逻辑推导

二分查找算法： 也称为二分搜索算法，是一个很巧妙的算法，在实际开发中我们会经常使用到这个算法，能在很大的数量有序不重复集合下快速查找到一个元素，每次查找一次如果不符合命中条件的，那么参入搜索的集合就会被折半一次，也就是下次搜索的时候数量会少一半，原理如下图：

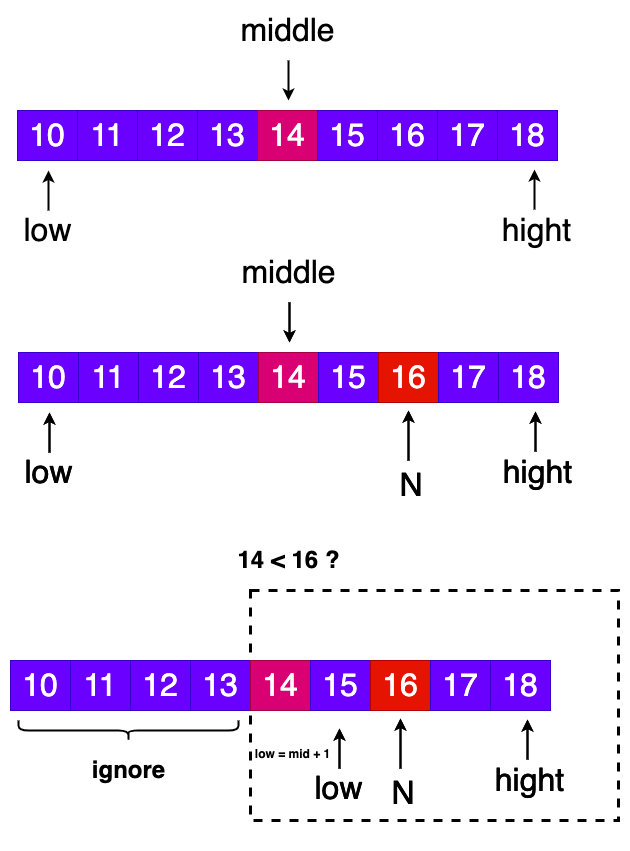
代码实现

首先要在被排序的数组里面定义两个指针，分别是low和high，还有一个middle指针，这个指针是随机的取low和high指针区间的随机数。

然后每次搜索就是看需要查找的n是否等于middle指针上的元素，如果等于那么就是命中查找到元素直接返回即可。

否则就看middle是否小于n，如果小于那么就把low指向middle + 1处，如果大于就把high指向middle - 1处。

package main

import "fmt"

func main() {
    var arr []int = []int{10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20}
    index := binarySearch(arr, len(arr), 16)
    fmt.Println(index)
}

func binarySearch(arr []int, len, n int) int {
    // 初始化两个指针
    low, high := 0, len - 1
    // 两个指针的关系必须是low小于等于high
    for low < high {
        // 取中轴
        middle := low + ((high-low)>>1)

        if arr[middle] == n {
            return middle
        }

        // 如果middle小于n就说明不在middle前面的范围内
        // 如果middle大于n就说明不在middle后面的范围内
        if arr[middle] < n {
            low = middle + 1
        } else {
            high = middle - 1
        }

    }

    return -1
}

需要注意的是low + ((high-low)>>1) = low + (high-low) / 2这行代码，这行代码是为了防止有时候我们需要搜索的数据量太大，经过计算得出来的值会超过int类型的表示范围，所以这来采用优化，位运算也是比传统除法性能要高很多的。

下面是递归版本的实现：

package me.ibyte.sorting;

public class BinarySearch {

    public static void main(String[] args) {
        int[] arr = { 10, 11, 12, 13, 14, 15 ,15};
        int index = bsearch(arr, 14, 0, arr.length - 1);
        System.out.println(index);
    }

    public static int bsearch(int[] arr, int n, int low, int hight) {

        if (low > high) {
            return -1;
        }

        int middle = low + (high - low) / 2;

        if (arr[middle] == n) {
            return middle;
        }

        if (arr[middle] < n) {
            return bsearch(arr, n, middle + 1, high);
        } else {
            return bsearch(arr, n, low, middle - 1);
        }

    }

}

以上是我的实现代码，掌握了二分查找算法的思想其实用代码写起来就很容易，把思路转换成代码实现就可以了，如果不能理解自己可以先画一下图，例如上面就是我自己画的图，图画完就清晰多了，或者可以看看这个视频讲解二分搜索算法。

优点：在一定数据量下查找数据是O(logN)，会很快的就能查找到目标数据。

缺点：数据必须全部是静态的并且数据量占用内存不能太多，二分查找依赖于数组，数组存储是连续的，如果数据规模较小可以使用暴力顺序遍历查找，如果数据量较多并且在操作的时候会动态发生修改建议使用二叉搜索树或者哈希表。

其实二分查找算法最核心思想是每次进行一轮搜索，数据范围会缩小n/2，这个和插入排序的进阶版本希尔排序的思想差不多。每进行一轮会在原始数组上进行数据缩减，而不是传统方式的O(n)一个一个去查找目标值，而是带着有条件有跨度去搜索，这里条件就是原数组有序并且每一轮都能确定目标数据所在的范围。

变体问题

二分查找本质也是分而治之的应用，本身如果搜索查找一个元素的话没有什么难度。还有一部分二分查找算法应用就是使用二分查找在有重复的数据段里面做模糊查找。例如[12,13,14,14,14,15,16,17]，这个数组里面有3个14，如果要查找其中一个14出现的位置，那么就是模糊查询了，因为要其他的而外条件才能正常工作，相关的算法问题如下几个：

找出某个元素第一次出现的位置：

package me.ibyte.sorting;

public class FirstAppear {

    public static void main(String[] args) {
        // 查找到14第一次出现的位置
        int[] arr = { 10, 11, 12, 13, 14, 14, 14, 15, 16 };
        int index = firstAppear(arr, 14, 0, arr.length - 1); // 4
        System.out.println(index);
    }

    public static int firstAppear(int[] arr, int val, int low, int high) {
        int middle = 0;
        while (low < high) {
            middle = low + (high - low) / 2;
            if (arr[middle] < val) {
                low = middle + 1;
            } else if (arr[middle] > val) {
                high = middle - 1;
            } else {
                // 如果在一个位置是就是头部说明就在头部
                // 如果是在中间某一部分出现那么就看看前面是否重复如果重复就找打了
                if (middle == 0 || arr[middle - 1] != val) {
                    return middle;
                } else {
                    // 如果上面条件都不满足，说明要找的元素在左半部分，砍掉右边部分
                    high = middle - 1;
                }
            }
        }
        return -1;
    }
}

找到最后一次出现的位置：

package me.ibyte.sorting;

public class LastAppear {

    public static void main(String[] args) {
        // 查找到14最后一次出现的位置
        int[] arr = { 10, 11, 12, 13, 14, 14, 14, 15, 16 };
        int index = fastAppear(arr, 14, 0, arr.length - 1); // 6
        System.out.println(index);
    }

    public static int fastAppear(int[] arr, int val, int low, int high) {
        int middle = 0;
        while (low < high) {
            middle = low + (high - low) / 2;
            if (arr[middle] < val) {
                low = middle + 1;
            } else if (arr[middle] > val) {
                high = middle - 1;
            } else {
                // 本来就是最后一个了那就直接返回，如果不是就看后面的元素是否一样，不一样则返回
                if ((middle == arr.length - 1 || arr[middle + 1] != val)) {
                    return middle;
                } else {
                    // 一样说明前面的范围可以排除掉，继续往后搜索
                    low = middle + 1;
                }
            }

        }
        return -1;
    }

}

其实二分模糊搜索主要是考查，使用者是否掌握了基础二分查找的算法思想。模糊查找核心的点就是：看能不能找出符合元素位置的前后关系条件，根据元素前后关系条件做出查找，在每轮查询的过程中，能确定目标元素有可能所在的区间，排除不存在的区间，不断的缩小可能存在的区间范围，下面是我画的一张图，如果阅读我blog朋友也能自己画出这样的图，那说明应该是掌握了二分查找最基本区块划分的思想。

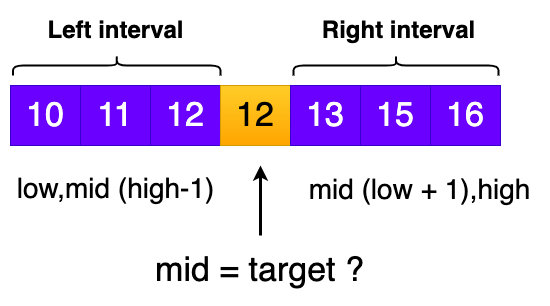
下面是一些带有双重查询条件的问题，例如查找第一个大于或者等于14的元素：

// 查找第一个大于等于target的元素
public static int greaterOrEqual(int[] arr, int target, int low, int hight) {
    int middle = 0;

    while (low < hight) {

        middle = low + (hight - low) / 2;

        // 这个满足大于等于
        if (arr[middle] >= target) {
            // 但是要求是第一个或者前面一个元素小于要查找的元素，那么就是这个mid了
            if (middle == 0 || arr[middle - 1] < target) {
                return middle;
            } else {
                hight = middle - 1;
            }
        } else {
            low = middle + 1;
        }

    }

    return -1;
}

查找最后一个小于或者等于某值的元素：

public static int lessThanAndEqual(int[] arr, int target, int low, int hight) {
    int middle = 0;

    while (low < hight) {
        middle = low + (hight - low) / 2;
        // 如果大于就抛弃右部分
        if (arr[middle] > target) {
            hight = middle - 1;
        } else {
            // 然后看看是不是最后一个了，再看后面一个是不是大于前面一个
            if (middle == arr.length - 1 || arr[middle + 1] > target) {
                return middle;
            } else {
                low = middle + 1;
            }
        }
    }

    return -1;
}