树是一个非线性结构,日常很多东西都和树这个结构类似,例如:企业人员组织架构,操作系统的文件目录,如果这些信息被高度抽象到某种程度那么就是一种数据结构的应用了,这篇文章讲整理一下 树 的知识。
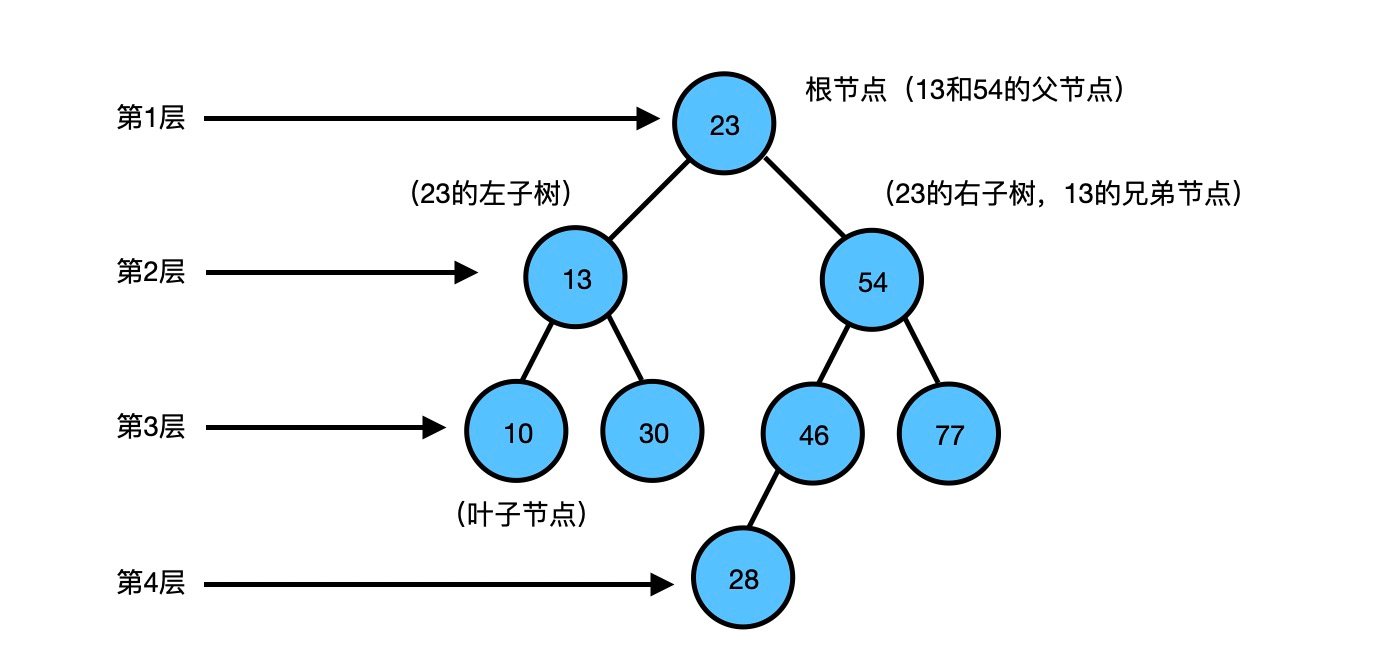
树最简单的结构组织方式就是二叉树,二叉树是树里面应用最简单的一种树型结构,其特征就是每个节点有2个子节点或者说一个节点,也可以有一个上级节点,如果当前节点没有子节点但是有父节点那么可以认为是叶子节点。节点之间的关系就是:层次关系,左右关系,层次关系是子节点和父节点之间的关系,左右关系是父节点下的左右节点之间的关系,如下图:
关于树的一些名词有: 高度 、 深度 、 层数 ,这些可以用来形容一个树的元信息。
- 节点的高度:节点到叶子节点的最长路径的长度也就是边数。
- 节点的深度:根节点到这个节点的路径长度的边数。
- 节点的层数:节点的深度加上1。
- 树的高度:也就是根节点的高度。
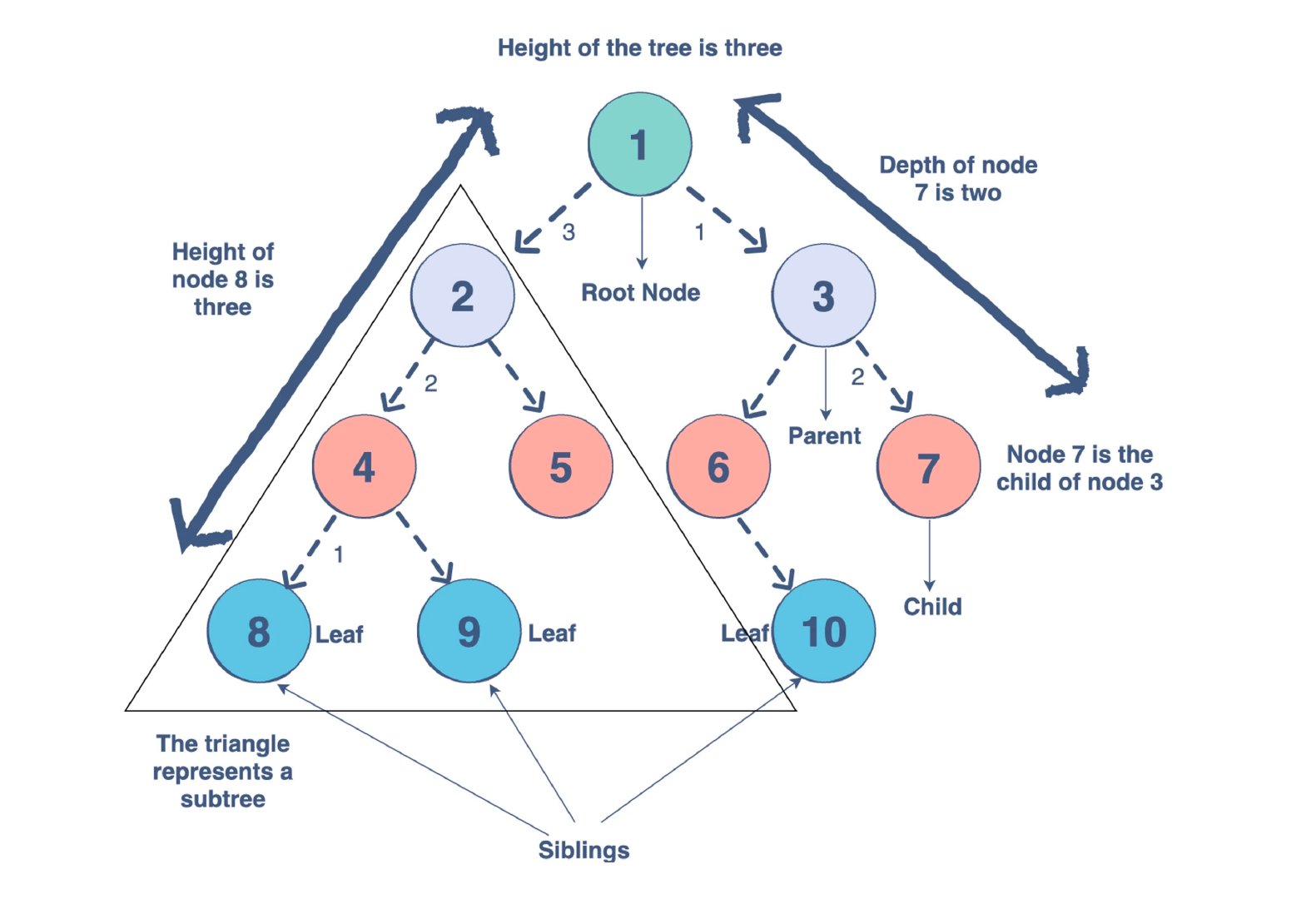
上图就是一颗树的结构图,此结构不限于二叉树所有树形结构都适用。
树的存储
树的存储方式有两种,一种是链式存储,一种是数组存储;链式存储如下图,一共 3 个字段,一个字段存储数据,另外两个字段存储左右子节点:
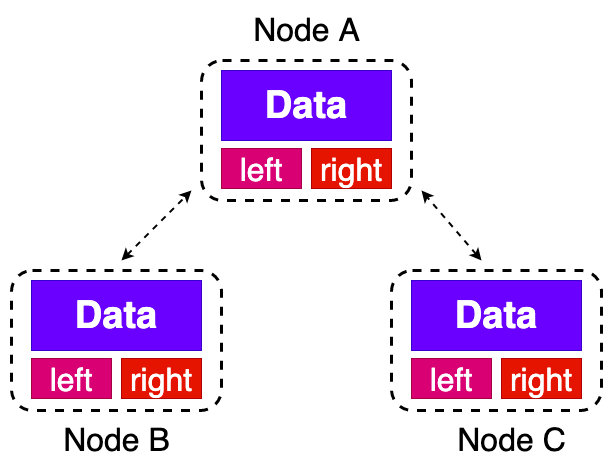
另外一种就是使用数组进行存储,连续空间存储,如下图:
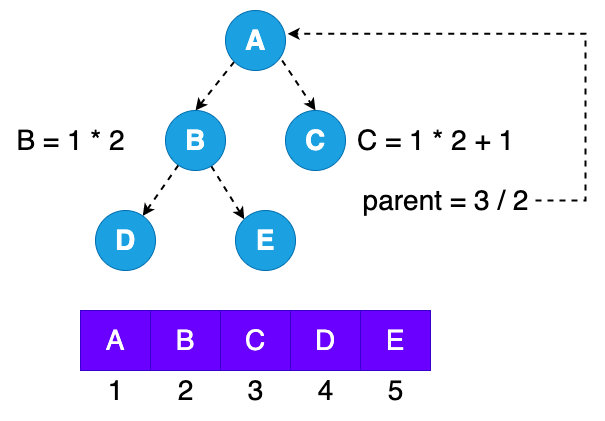
上面是使用数组连续空间存储的话不需要额外的空间占用去存储左右孩子节点的 child 的指针,而是通过数组的下标去访问数组上的元素,而下标访问是很特殊的公式如上图我所画的,计算公式很简单: 父节点 = 当前节点下标 / 2,左孩子节点 = 当前下标 2,右孩子节点 = 当前下标 2 + 1;当然有一个前提是数组存储的时候根节点下标为1,而不是0,如果是零的话公式还需要额外计算,大多数1为根节点下标,0有的话空出来,浪费一个位置空间没有什么特殊的。
两种存储方式利弊: 第一种使用链式存储的话,在数据节点需要加入树中的时候可以动态分配内存,而数组的方式则要在使用前提取分配一堆连续的内存,然后去存储元素,因为数组的特殊性,如果数中某些子节点只要单一的孩子节点,那么数组对应上的位置为空,要预留这些位置,不能充分使用内存,如果是完全二叉树情况下推荐使用数组,对于非完全二叉树的情况下还是使用传统链式存储方式,这个可能要根据使用的时候场景进行分配。
树的应用
树最典型的应用就是二叉搜索树了,二叉搜索树特点就是一个节点最多只有两个节点,也可以只有一个节点,而左子节点比父节点本身小,右子节点比父节点大。
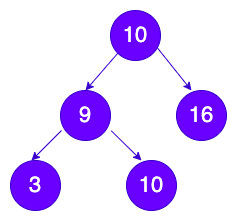
如上图我所画的就是一个典型的完全二叉搜索树,并且满足左节点小于父节点,右孩子大于父节点的要求,用代码实现的话,用链式存储实现是最为简单的,下面是链式存储实现代码:
package tree
import "github.com/auula/coffee"
type Node[T coffee.Number] struct {
Data T
LeftChild, RightChild *Node[T]
}
type BinaryTree[T coffee.Number] struct {
Root *Node[T]
Size int
}
func (bt *BinaryTree[T]) Insert(v T) {
if bt.Root == nil {
bt.Root = &Node[T]{Data: v}
return
}
node := bt.Root
for node != nil {
if v > node.Data {
if node.RightChild == nil {
node.RightChild = &Node[T]{Data: v}
return
}
node = node.RightChild
} else {
if node.LeftChild == nil {
node.LeftChild = &Node[T]{Data: v}
return
}
node = node.LeftChild
}
}
}
func (bt *BinaryTree[T]) Search(v T) *Node[T] {
node := bt.Root
for node != nil {
if v < node.Data {
node = node.LeftChild
} else if v > node.Data {
node = node.RightChild
} else {
return node
}
}
return nil
}
构造一颗二叉搜索树很简单,先是构造根节点,然后根据需要被插入的节点的值构造左右子节点,搜索方式也是根据节点大小进行的,时间复杂度为O(logN)。
func Previous[T coffee.Number](node *Node[T], channel chan *Node[T]) {
if node == nil {
return
}
channel <- node
Previous(node.LeftChild, channel)
Previous(node.RightChild, channel)
}
func Intermediate[T coffee.Number](node *Node[T], channel chan *Node[T]) {
if node == nil {
return
}
Intermediate(node.LeftChild, channel)
channel <- node
Intermediate(node.RightChild, channel)
}
func Back[T coffee.Number](node *Node[T], channel chan *Node[T]) {
if node != nil {
return
}
Post(node.LeftChild, channel)
Post(node.RightChild, channel)
channel <- node
}- 前序遍历:先根,再左,后右
- 中序遍历:先左,再根,后右
- 后序遍历:先左,再右,后根
以上是树的三种遍历方式的代码实现,前序、中序、后续遍历实现,对应遍历的方式就是对元素组织的方式,如果要把数中的元素排序输出的话可以使用 中序遍历 ,这就是利用二叉搜索树和遍历方式的特性。
相比上面3中遍历方式,还有两种遍历方式:
- 深度优先:需要从左子节点开始遍历输出,每个分支先往叶子节点走,然后递归顺序和中序遍历一样。
- 广度优先:按照左右子同层节点开始遍历输出,递归是每个子树进行,先左,后右,再往下层走。
删除节点
二叉树搜索树另外一个点就是对节点进行删除调整操作,删除操作相比添加和搜索节点相对来说复杂一点,而且树的结构形状有多样的。例如:直接删除叶子节点这是最简单的,直接操作父节点的指针即可完成,而另外一种就是有左右孩子节点,这种情况就是移动右子节点到当前节点位置如下图:
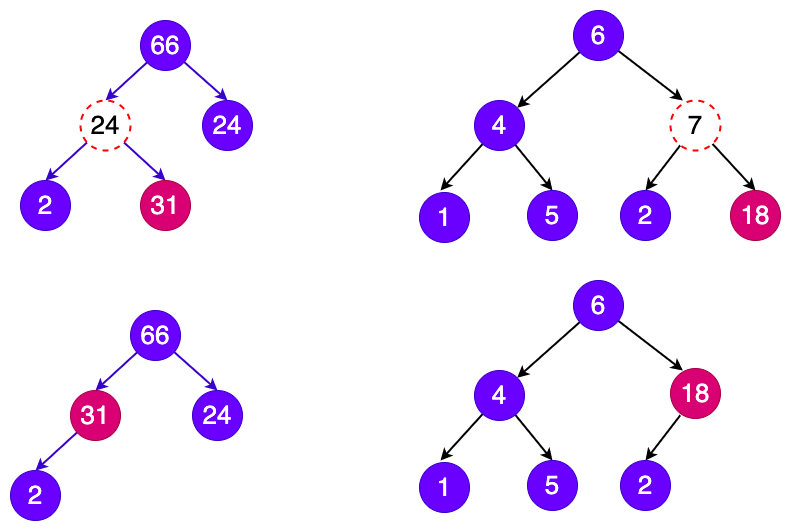
func (bt *Tree[T]) Delete(v T) *Node[T] {
return delete(bt.root, v)
}
func delete[T coffee.Number](node *Node[T], v T) *Node[T] {
if node == nil {
return nil
}
if v < node.Data {
node.LeftChild = delete(node.LeftChild, v)
} else if v > node.Data {
node.RightChild = delete(node.RightChild, v)
} else {
// 如果找到了看看有没有左右子节点
if node.LeftChild == nil {
return node.RightChild
}
if node.RightChild == nil {
return node.LeftChild
}
// 不断的在右边找最小节点,然后换上去
minNode := node.RightChild
for minNode.LeftChild != nil {
minNode = node.LeftChild
}
node.Data = minNode.Data
// 换上去直接再把右子节点最小值删除掉
node.RightChild = delete(node.RightChild, minNode.Data)
}
return node
}删除逻辑: 删除节点逻辑和查找节点逻辑有点类似,区别在于要删除节点,首先要判断要删除的元素在树的左边还是右边,如果在左边,那么就不断的递归往下找。递归逻辑就是 每次要进行区分在左还是在右 ,如果匹配到节点,那么就要有没有左右子节点,然后在右子树找到最小值替换到节点上,然后再去右子树把值删除掉,测试代码如下:
package main
import (
"fmt"
"github.com/auula/coffee/bst"
)
func main() {
tree := bst.New[int]()
tree.Insert(10)
tree.Insert(9)
tree.Insert(16)
tree.Insert(3)
tree.Insert(10)
tree.Delete(9)
channel := make(chan *bst.Node[int])
go func() {
bst.Previous(tree.Root, channel)
close(channel)
}()
for v := range channel {
fmt.Println(v)
}
}元素重复
上面我整理了二叉搜索树的普通情况,元素都是不存在重复的情况比较好处理,如果遇到重复的元素,要怎么处理呢?
第一种处理方式很简单: 和哈希表设计一样遇到元素一样的就使用一个数组存储或者说使用链表存储,类似于解决哈希表的元素冲突方式。
第二种处理方式复杂: 需要把插入的元素放到相等元素的右子树,也就是当插入完成之后,右子节点的字数里面有和当前元素相同的元素存在,这样查找元素的时候需要注意要查找整个树节点,范围为第一个重复元素出现位置到叶子节点位置。
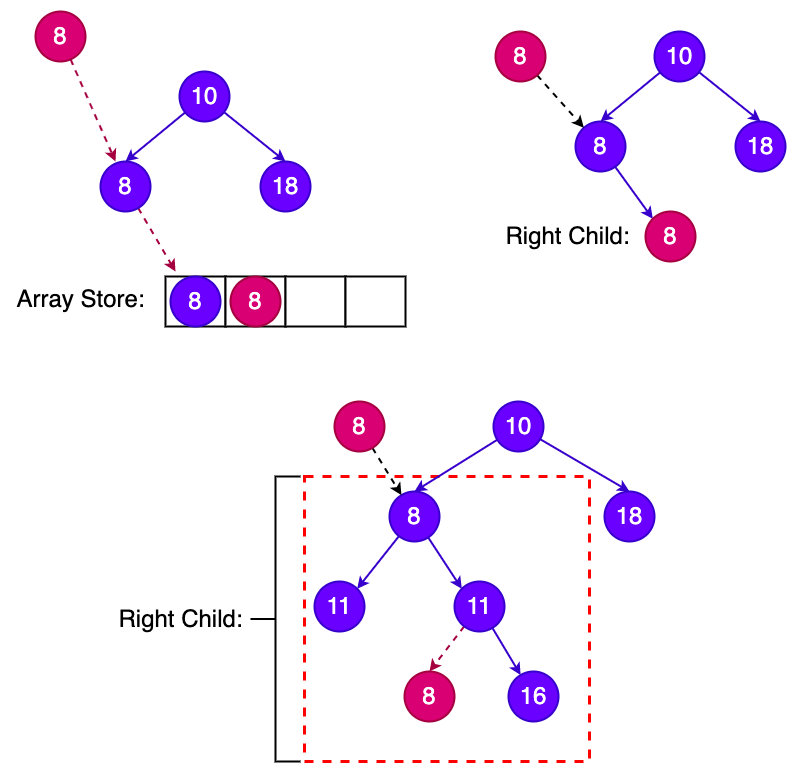
树的平衡
二叉搜索树在数据分布的比较均匀的情况下,树的节点相对来说查找速度就很快 O(logN) ,如果树上元素不能均匀分布,偏向另外一边那就退化成链表 O(N) 了,如下图:
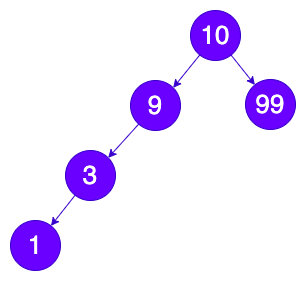
为了解决这些问题,那么就要针对这颗树,进行调整了,很多计算机前辈提出来了平衡树概念:红黑树,AVL 树,这些都是为了解决树元素不能平衡分布的而提出来的新型树元素组织方式。但是为了满足节点平衡每次插入数据的时候需要进行数据调整,每次插入节点都需要维持平衡性,但是调整过程很繁琐。
B+树
B+树也是B树延伸过来的,这里的 B 是指的是 Balanced 意思。B+ 树最常见的用处就是在数据库索引领域,树的节点除了叶子节点存储具体的数据以外,上层的节点全部用做索引的(稠密索引),上层的节点都是区间索引,可以通过二分查找法进行查找数据的。
B+ 树的高度和查询次数的 io 成正比,B+ 树解决的问题传统索引可能全部把所有索引存储在内存里面,但是 B+ 树把根索引存放在内存,其他节点可以存储在硬盘里面。对应一个 B+ 树的层次来说,每层节点越多,那么数的高度就越小,对应的 io 操作次数也会小。
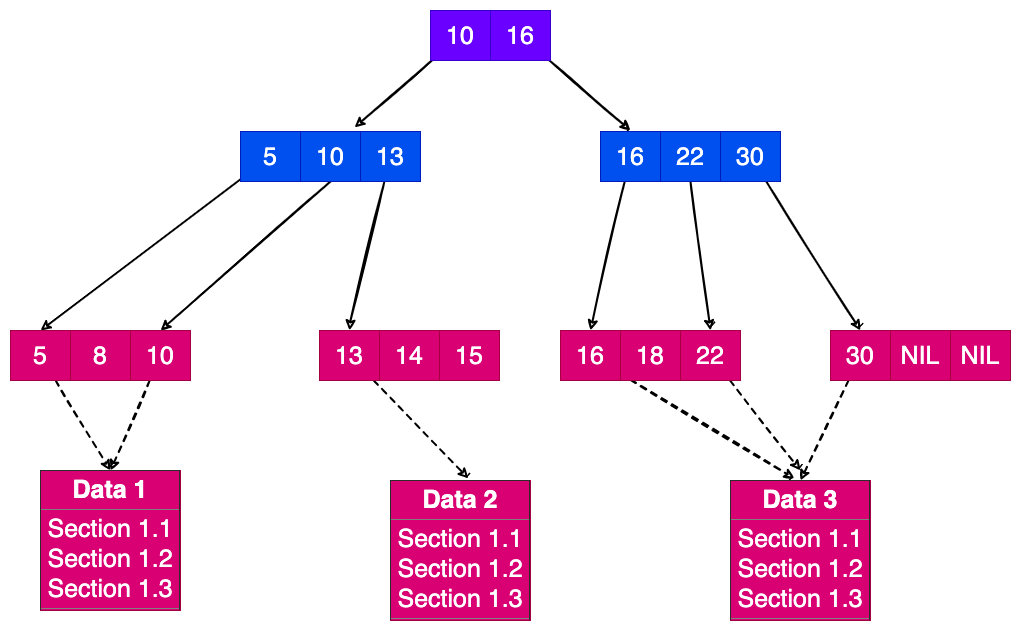
其实抽象到一定程度,其实解决的问题,和跳表一样,把一个有序链表分割成多个段。
B+ 树的缺点就是,如果当叶子节点的元素个数小于2的时候需要触发一次合并,合并操作就是把多就叶子节点合并成一个节点,合并过程比较难用实现,当然这是我个人这么认为的,做到了解工作原理就可以。
- B+树由
m叉查找树和叶子结点有序链表组成的。 - 每个节点中子节点的个数不能超过
m个并且也不能小于m/2个。 - 根节点的子节点个数可以不超过
m/2,这是一个例外。 - 一般情况下根节点被存储在内存中,其他节点存储在硬盘中。
为了保证每次操作的时候节点符合以上规则,需要动态调整节点,写入操作的时候数据,会变慢。相对于B树的差别在于节点不存储数据,所有数据存储在叶子节点中,其他节点为数据索引查找节点。
小 结
树和哈希表都可以起到搜索一个元素的效果,但是二者有什么不同呢?如果从实现角度来讲的话,二叉树实现起来比哈希表简单,设计一款好的哈希表要考虑存储方式,哈希函数,哈希冲突并且元素是无序的,等其他一些因素。而设计一颗二叉树紧要知道怎么去组织节点层次关系就可以了,相当于元素输出方式,二叉树有多种:前序遍历、中序遍历、后序遍历。

